How I get all my students to be good at math
As a mathematics educator for the last seven years, I can attest that most folks believe they either are or are not “math people.” And that idea of innate math ability is very harmful to both those who believe they possess it and to those who believe they don’t. Furthermore, our new era of accountability (read test-taking) perpetuates this fallacy and clouds the message we want our students to receive in math class.
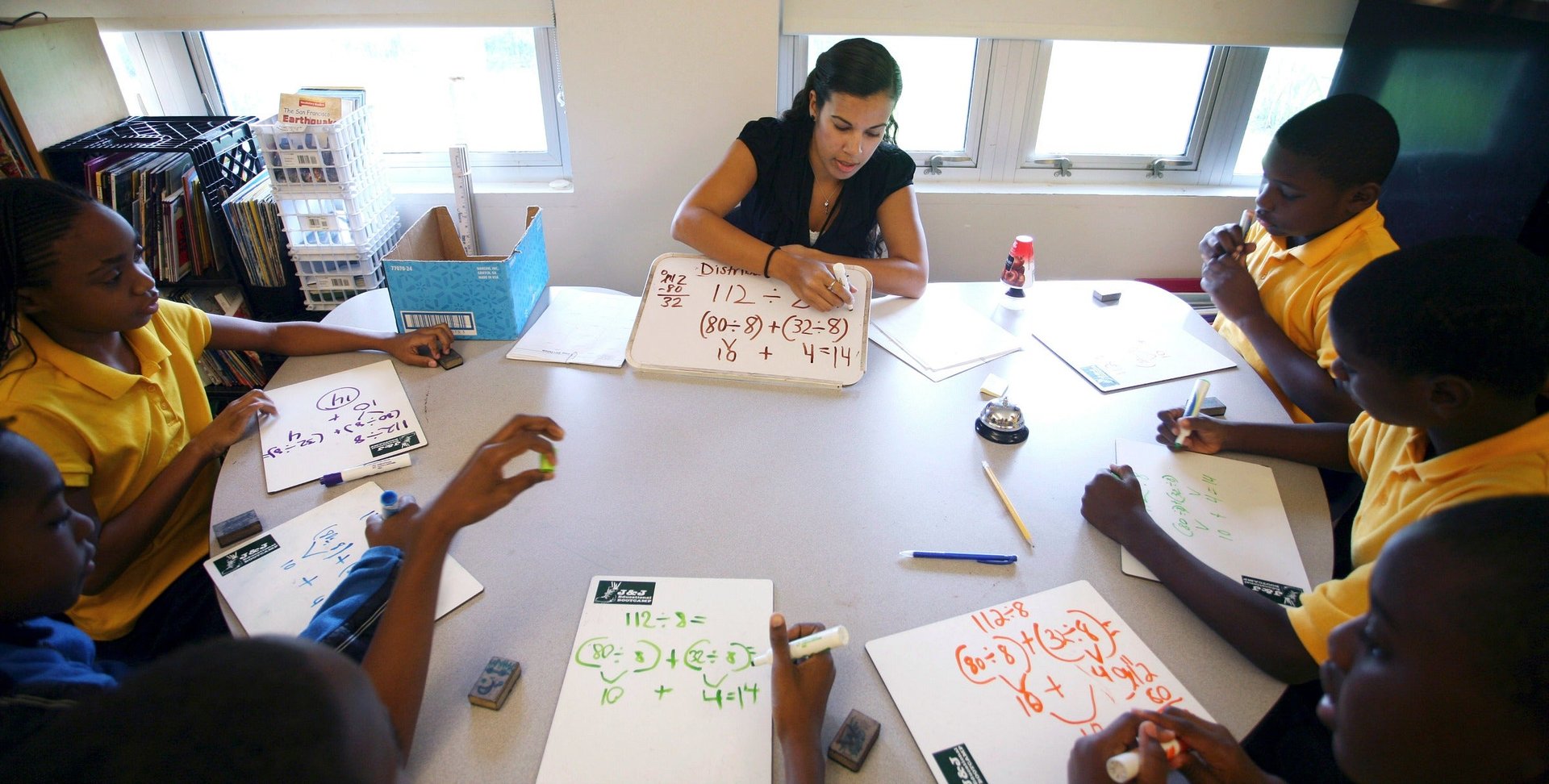
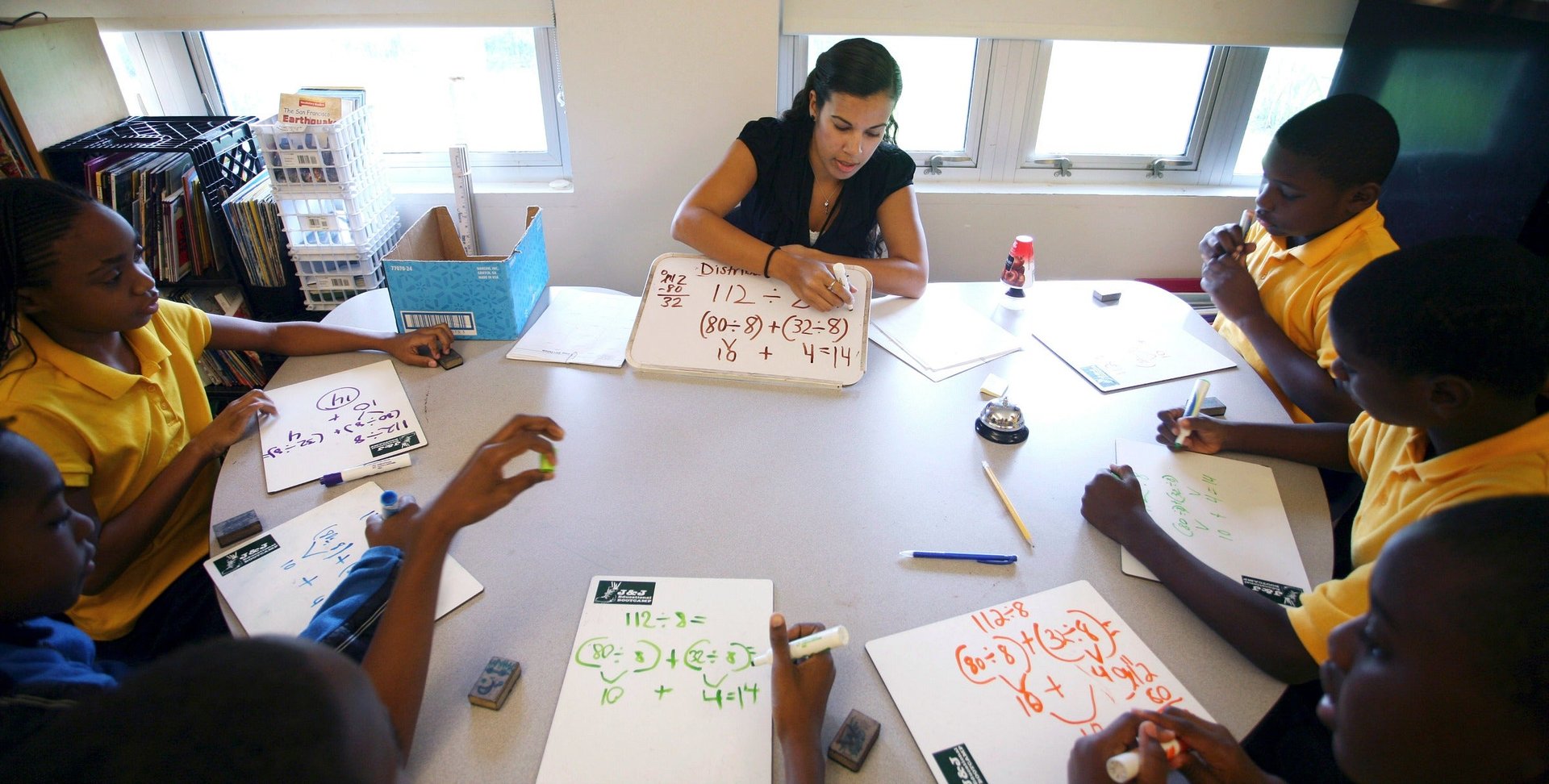
As a mathematics educator for the last seven years, I can attest that most folks believe they either are or are not “math people.” And that idea of innate math ability is very harmful to both those who believe they possess it and to those who believe they don’t. Furthermore, our new era of accountability (read test-taking) perpetuates this fallacy and clouds the message we want our students to receive in math class.
Not all the same: Algebra is not the same as geometry
There is most certainly no such ability that allows some students to pass algebra and others to fail. This argument is made forcefully and articulately in Noah Smith and Miles Kimball’s recent article in Quartz, so I won’t rehash the point except to say that math draws on a huge range of cognitive processes. Those who are weak at arithmetic can be very good at abstract mathematics. Many students who hate algebra love geometry. Each student I have taught, including those designated as gifted and those diagnosed with severe learning difficulties, has had strengths that helped him or her learn some topics in mathematics easily, and has had weaknesses that made learning other topics in math incredibly difficult. I tell all students alike that math requires perseverance and a willingness to take risks and make mistakes. These qualities are much more predictive of mathematical success than innate ability (if such a thing exists). Students often place themselves in the “not math people” category before they even know that each math teacher teaches it differently, or that different topics in math draw on different skills.
Overconfidence is just as harmful
How else is the belief harmful? For those who believe they are not “math people,” it makes them feel helpless. Math requires effort, patience and time. You have to believe that eventually, you will be able to understand. You have to sort through what you understand and what you don’t. You have to then formulate a good question and be courageous enough to ask the teacher to answer the question in front of a classroom, admitting that you don’t understand something in front of your peers—some of whom groan and say, “But it’s sooo easy. How come you don’t get it!?” It’s so much easier just to say,” Hey, I wasn’t born with this mystical mathematics ability so it’s not my fault.” But you would be wrong.
Math can make even the smartest people feel dumb and believing in an intrinsic mathematics ability isolates the stupidity. It’s not me who’s stupid, it’s just one part of my brain that’s stupid—and there’s nothing I can do about that part of my brain so I don’t need to humiliate myself in class tomorrow by asking the question I want to ask. People with this mindset keep getting further and further behind in math because if they don’t feel themselves capable of learning something, they’ve let themselves off the hook and invest their mental energy in other realms.
Further, those who think of themselves “math people” can suffer from overconfidence. Recently I’ve been seeing a lot students (often male) claiming they know and understand everything so they don’t need to practice or take notes. Their homework and test grades are still abysmal. I believe some of this overconfidence comes from the testing they’ve had to endure. These kids are bright and have learned test-taking skills easily so their standardized test scores are consistently high. But truly understanding math requires effort and perseverance and isn’t worth the time if they can still perform well on tests. I have four students in one of my classes who frequently cite their high test scores as an excuse for not doing homework, not taking notes, or performing poorly on free-response tests. They believe themselves “math people” because they’ve been successful on the one measure the state cares about and they see no need to put more effort in.
Do we judge? Or do we educate?
Standardized testing helps perpetuate this fallacy on multiple fronts. There are two diametrically opposed goals we as a society have for public education and because we can’t choose which goal is more worthy of attainment, we’ve been bogged down in ideological battles. Schools can be about sorting, or about educating. I think right now we want them to be about both, but this is impossible. Schools focused on sorting are obsessed with fairness. Only students who produce “A” work (as arbitrarily decided by the teacher or the state) get “A’s.” Honor roll highlights the best students, standardized tests rank schools and designate children as “below basic,” “basic,” “proficient,” or “advanced.” These rankings make it easier for colleges and employers to sort out the students they want from those they don’t. In a world where schools are designed to sort out those who are going to college, those who are going into vocations, those who are going into unskilled labor and those who are going to prison, belief in innate math ability is appropriate. Those who have it are sorted into more difficult math classes, those who don’t stop taking math as soon as possible. We test, judge and sort. Theoretically, the fear that they will be sorted into an undesirable category is what keeps some students motivated.
Our educational goal should be to help all students learn as much and as deeply as they possibly can, and to instill in them a love of learning. In Diane Ravitch’s new book, Reign of Error, she cites a study conducted in the 1980s by Richard J. Murnane and David K. Cohen. Teachers given poor evaluations performedmore poorly, while those given positive evaluations, even if undeserved, worked harder and were more willing to seek help for their problems. Though this study was about teachers, I don’t see why it can’t apply to students as well. When I give students a lot of credit for persevering showing them that their efforts are valuableearly in the term, I get higher quality work from them as the term progresses because they don’t give up when things get hard. Using grades to encourage perseverance rather than to sort or judge means that I don’t need to inflate their grades at the end because the accumulated effort they’ve put in has allowed them to truly master the material.
There’s a lot of research (see Daniel Pink’s TED talk on the puzzle of motivation) that says people perform poorly on difficult cognitive tasks when there are extrinsic rewards for the successful accomplishment of those tasks. Students tend to have more difficulty thinking in math when they’re under time constraints, extrinsic pressure or are fearful of being judged. My goal is to remove these pressures to help students perform better.
Here’s an example demonstrating that rewarding students based on effort encourages them to continue to work hard. I taught a student for three years, through pre-algebra, algebra and geometry. She struggled in pre-algebra and algebra 1, almost always failing tests the first time and only passing thanks to credit for consistently doing homework, coming in for tutoring, and doing test corrections. She slowly increased in confidence and became a very capable math student in geometry (the best in the class at proofs). Here’s an e-mail she wrote me after I left:
I wanted to thank you. Even though you are not my teacher anymore, you still help me all the time. You wrote in my yearbook to remember that I am good at math, and I always go back to that and it actually helps me when I am stressed about algebra 2. Whenever I think about it, I feel as though I can push through and actually do it. I am doing pretty well in it so far and I owe part of that to you.
She continues to receive low standardized test scores because she performs poorly under pressure.
In math especially it’s easier to judge rather than to coax and reassure. Because there are always right and wrong answers, it’s so easy for standardized tests to sort students into those who can get the right answers and those who can’t. Standardized testing disregards the effort students have exerted and they deemphasize the processes of math. Students are left feeling helpless if they can’t achieve. These tests judge students based on an arbitrary benchmark set by state politicians who have little understanding of what developmentally appropriate skills truly are. Like novice chess players, students learn the rules of math and combine and manipulate them to learn how to play the game. Like a novice chess player, a math student will learn just as much if not more from her failures as from her successes. Focusing on the process of math helps both low achieving and high achieving students learn true mathematical logic and not get discouraged because they can’t reach a right answer, or bored because reaching the right answer is too easy. Many students know how to get the right answers on standardized tests but don’t know how to think about math.
Parents, don’t be a part of the problem
What can we do about helping students focus more on the process of math and on persistence, less on labeling themselves as “math people” or “non math people?” First of all, we adults need to model different behavior than I’ve seen demonstrated in my years as a teacher. The myth of innate math ability is perpetuated from generation to generation. When I tell adults I’m a math teacher, 90% of the time I get the comment, “I’m not a math person,” accompanied by a look of sheer terror and either tentative stories of math humiliation or an abrupt change of subject. Once, a visiting school guidance counselor told my students, to my horror, that he hated math and not to listen to me when I told them math was important. They would never need it in the “real world.” I’ve been writing this article in coffee shops, occasionally making comments to my husband. On three successive visits strangers have overheard my comments to him, asked me what I’m doing, then told me that there definitely are ‘non math people’ and that I’m looking at one. Upon elaborating my position though, all three changed their minds and have admitted the importance of math in their own lives (one was an industrial architect).
My students’ parents also believe in this fallacy and sometimes, perpetuate an anti-math attitude. They don’t use math at work, can’t help their students with their math homework, and are convinced themselves that they’re “not math people”. Furthermore, because these adults have survived without math, they tell their children that math isn’t necessary in the workplace. These adults have made their choices. They chose/were forced into careers where math wasn’t required and so they convince their children that only the “math people” will ever get anything out of a comprehensive mathematics education. Our job as role models is to give our students the freedom to make their own choices, including lucrative choices in fields that require math. In my education courses, we were always told that modeling is more powerful than teaching. Adults are modeling this self-defeatist attitude.
If at first you try, you will succeed
In the classroom, we as teachers need to remove some of the stress we place on students and give them the freedom to fail. So many crossword puzzle enthusiasts (my whole family) look forward to checking their solutions against the key printed in tomorrow’s newspaper while so many students dread seeing their returned math test. Why? Because the crossword puzzle enthusiast knows he will learn more about doing crossword puzzles if he checks the key carefully, whereas the math student sees the returned test as a judgment about his intelligence. Students need to see that the attempt is just as valuable as the result. In my classroom, I award students credit for all problems they attempt, regardless if they got the correct answer. I refuse to let students turn in tests until every question is answered and double checked. I penalize late work, but I always accept it because who cares when they learn, just that they learn. I admit my own mistakes and award students when they catch me in a mistake. Finally, I find it productive to simply acknowledge that learning math can be challenging; telling a struggling student that a problem is easy is one of the most dispiriting things you can say to them. Education needs to be about personal growth and teaching students to enjoy and revel in their knowledge, not on grooming students and sorting them for a job market that may be entirely different in 10 years. If students learn confidence, flexibility and that they’re good at learning, they’ll be ready for anything.