A Golden Key for governments to bypass cryptography will never work, because math
In the name of protecting us against terrorists, law enforcement agencies want high tech companies to relinquish their Golden Keys—backdoors to their otherwise unbreakable encryption algorithms. It sounds like a reasonable request… until you look more closely.


In the name of protecting us against terrorists, law enforcement agencies want high tech companies to relinquish their Golden Keys—backdoors to their otherwise unbreakable encryption algorithms. It sounds like a reasonable request… until you look more closely.
Politicians around the globe tell us that for our own protection and security we must grant surveillance agencies a backdoor to today’s unbreakable encryption. While one is tempted to ask, glibly, if these leaders are ignorant, delusional, or dishonest—or all of the above—the question of granting or denying selective access to encrypted communications doesn’t lend itself to glib answers.
First, a look at the mathematical foundation of modern encryption.
Take two 70 digit prime numbers (copied from the University of Tennessee at Martin’s The Prime Pages):
Even the smallest of our personal computers — our phones — can compute the product instantly:

But going the other way—decomposing this product into its prime factors (a.k.a. factorization)—is disproportionately difficult. Even a sophisticated program such as Wolfram Alpha gives up after thinking about it for a few seconds:
The difficulty in factorizing the product of two prime numbers is an essential property of cryptography [emphasis and edits mine]:
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these integers are further restricted to prime numbers, the process is called prime factorization.
When the numbers are very large, no efficient, non-quantum integer factorization algorithm is known; an effort by several researchers concluded in 2009, factoring a 232-digit number (RSA-768), utilizing hundreds of machines took two years and the researchers estimated that a 1024-bit RSA modulus [cryptographic key] would take about a thousand times as long. However, it has not been proven that no efficient algorithm exists. The presumed difficulty of this problem is at the heart of widely used algorithms in cryptography such as RSA.
Bottom line: Modern cryptography is unbreakable. And even when computers become incrementally faster and threaten to break the code, we can simply move to longer keys (longer passwords, if you will).
Quantum computing, referred to in passing in the quotation above, offers a breakthrough in computing speed and, thus, in cryptanalysis. The discipline is still in its infancy, but when it finally materializes, won’t the immensely faster quantum computers throw us into the abyss of having to create unmanageably long keys? Fortunately, quantum cryptography will bring with it a new form of key encryption, as explained in this Scientific American blog post:
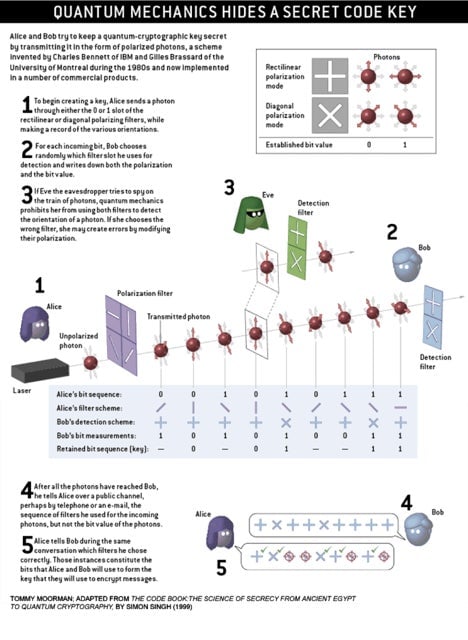
But that’s for the future. Today’s public-key cryptography has become so easy to implement that we now have communications services where the unbreakable encryption takes place inside the user’s device (smartphone, PC). The “public key providers”—Facebook, Google, Apple, etc.—have no knowledge of the users’ private keys and, as a result, they have no way to “open” the envelopes that contain the encrypted messages. (On page 38 of Apple’s iOS 9 security guide you’ll find a detailed explanation of the encryption mechanisms in the Messages app.)
Faced with unbreakable cryptography, government agencies everywhere clamor for a Golden Key that unlocks a “backdoor” into the messages that are exchanged by Bad People. Good Citizens understand the need; they urge their representatives to support the Golden Key laws. Problem solved.
No.
First, math is universal, so is the internet, and so is open source. Try googling “open source encryption”: You’ll get thousands of results, from academic papers to fully formed encryption tools. Anyone with a command of Linux can use or customize these unbreakable encryption tools.
(The availability of source code guarantees more than customization, it also helps detect surreptitious attempts to weaken the algorithms. This is no conspiracy theory—in 2013, the NSA was found to have provided a $10 million subsidy in exchange for weakening the encryption of an RSA product.)
The result is that the really determined Bad Guys can still avail themselves of encryption for which governments have no backdoors.
Second, the Bad Guys can also use steganography [edits and emphasis mine]:
Steganography is the practice of concealing a file, message, image, or video within another file, message, image, or video.[…]
The advantage of steganography over cryptography alone is that the secret message does not attract attention to itself […]. Plainly visible encrypted messages—no matter how unbreakable—arouse interest, and may in themselves be incriminating in countries where encryption is illegal.
Once you see the idea, you see ways to apply it. During World War II, German professor Zapp gave his name to the technique of photographically reducing messages to microscopic dots inserted as punctuation marks in innocuous-looking correspondence. Today, the binary text of an encrypted message is blended into a picture or a music file. A few kilobits of “noise” added to a 10 megabyte image is essentially undetectable… and how would you even know where to look in the unimaginably large jungles of pictures and videos uploaded everyday, everywhere, by everyone?
Third, Golden Keys are vulnerable. They’ll have to be shared between a number of agencies—meaning people—who need to access suspect communications. Even assuming “acceptable” diligence by their keepers, the keys can still be stolen by determined hackers working for other governments, terrorist organizations, or even domestic corporations who want a leg up on the competition. If banks and other financial organizations are forced to abandon unbreakable encryption, motivated criminals will go to great lengths to steal a Golden Key.
When, as is the case today, organizations use encryption technology for which there is no backdoor, we have safety. Once Golden Keys are forged (unintended pun, I promise), some will fall into the wrong hands. There’s no need to be sarcastic about possible government ineptitude or carelessness in large organizations: Experience shows us that backdoors get broken, especially when the payoff is large enough in financial or strategic terms.
Fourth, the good guys can turn. I won’t dwell too much on this because these are unpleasant thoughts, but… Today, my milquetoast opinions, behaviors, and associations are considered innocuous; a change of political wind and I could become an enemy of the state or, at least, suspect. My communications, all opened with the Golden Key, are mercilessly parsed by the Thought Police. The idea predates George Orwell; Cardinal de Richelieu (allegedly) put it in the starkest of terms: “If you give me six lines written by the hand of the most honest of men, I will find something in them which will hang him.”
“Damned if you do, damned if you don’t” seems to be our lot. Unbreakable encryption lets the Bad Guys converse securely, but Golden Keys are susceptible to various forms of theft through hacking, negligence, or persuasion.
I prefer really unbroken cryptography, but I don’t envy our elected officials who are caught in the dilemma.
This post originally appeared at Monday Note.